43. Pandas数据可视化-统计学相关图像

pandas数据在plot时可以通过kind形参来选择绘制图像的统计学相关的样式输出。

43.1 直条图

展示数据间相对区别、差别可以使用plot的kind参数。

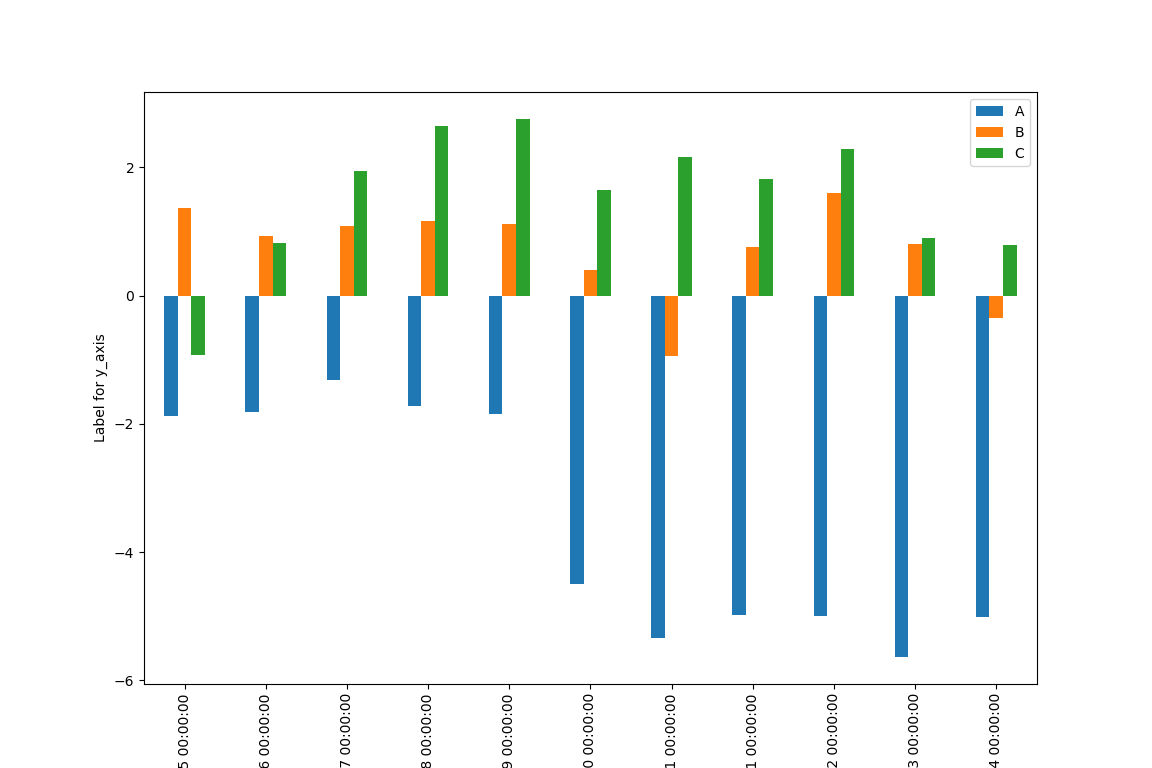
水平直条图，可以通过plot设置kind = “bar”实现。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
#print v
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
#print df
dfc = df.cumsum()
dfc.loc['2018-12-23':'2019-01-04'].plot(kind = "bar")
plt.xlabel("Label for x_axis")
plt.ylabel("Label for y_axis")
plt.show()

结果是这样的：

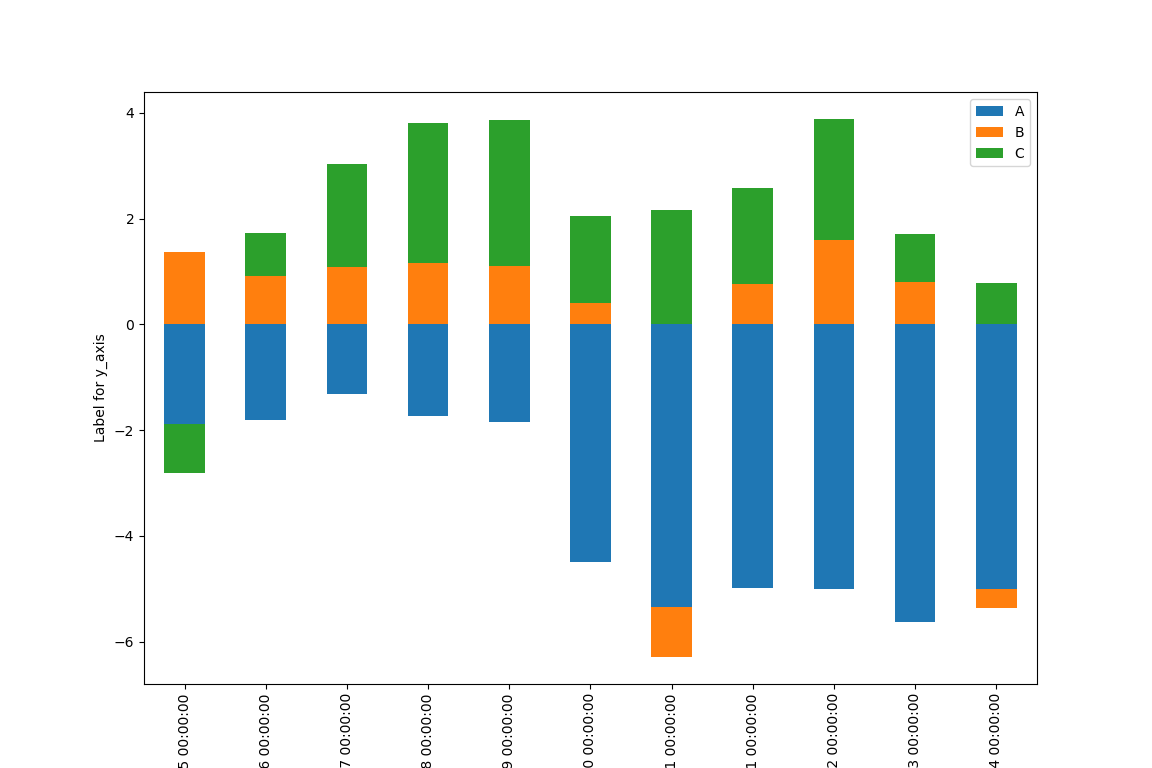
kind = “bar” stacked = "True"

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
#print v
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
#print df
dfc = df.cumsum()
dfc.loc['2018-12-23':'2019-01-04'].plot(kind = "bar", stacked = "True")
plt.xlabel("Label for x_axis")
plt.ylabel("Label for y_axis")
plt.show()

结果如下：

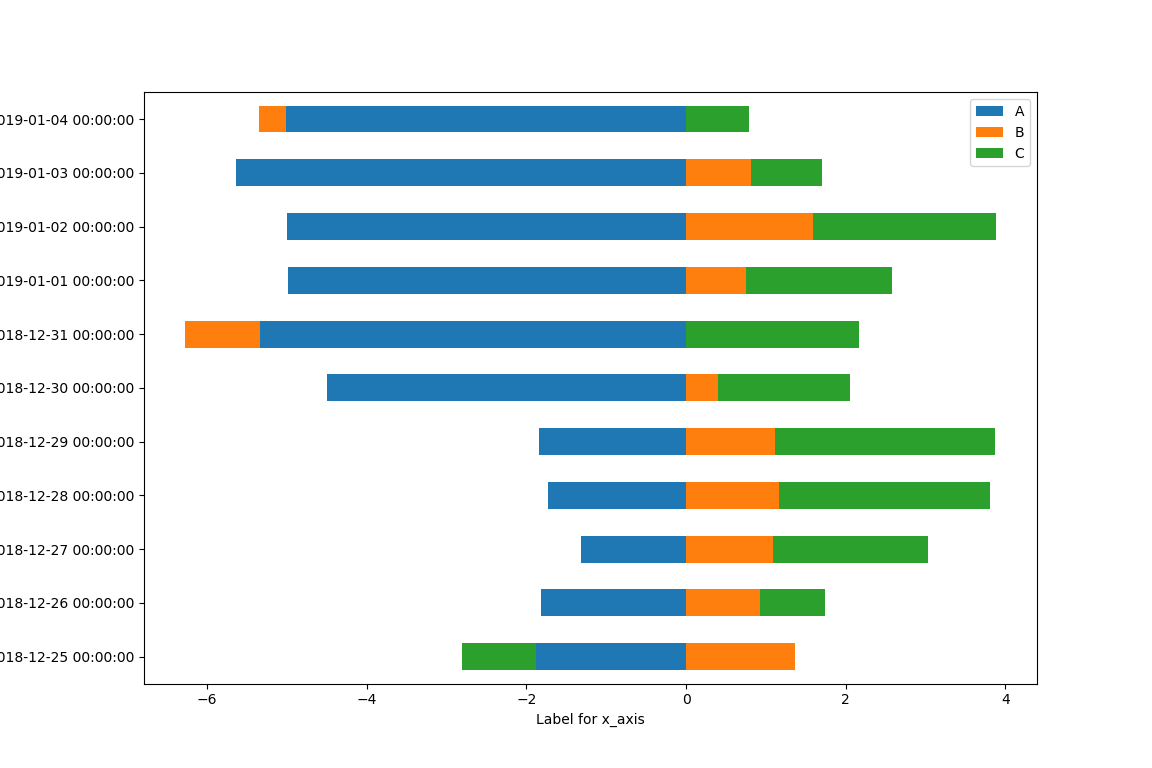
kind = "barh" stacked = "True"水平方向直条图

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
#print v
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
#print df
dfc = df.cumsum()
dfc.loc['2018-12-23':'2019-01-04'].plot(kind = "barh", stacked = "True")
plt.xlabel("Label for x_axis")
plt.ylabel("Label for y_axis")
plt.show()

执行效果如下：

43.2 直方图Histogram

直方图是数值数据分布的精确图形表示。是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况。一般用横轴表示数据类型，纵轴表示分布情况。可以使用hist函数来实现。

数据直接调用hist函数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
#print v
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
df.hist(bins = 100)
plt.show()

可以修改bins参数值。

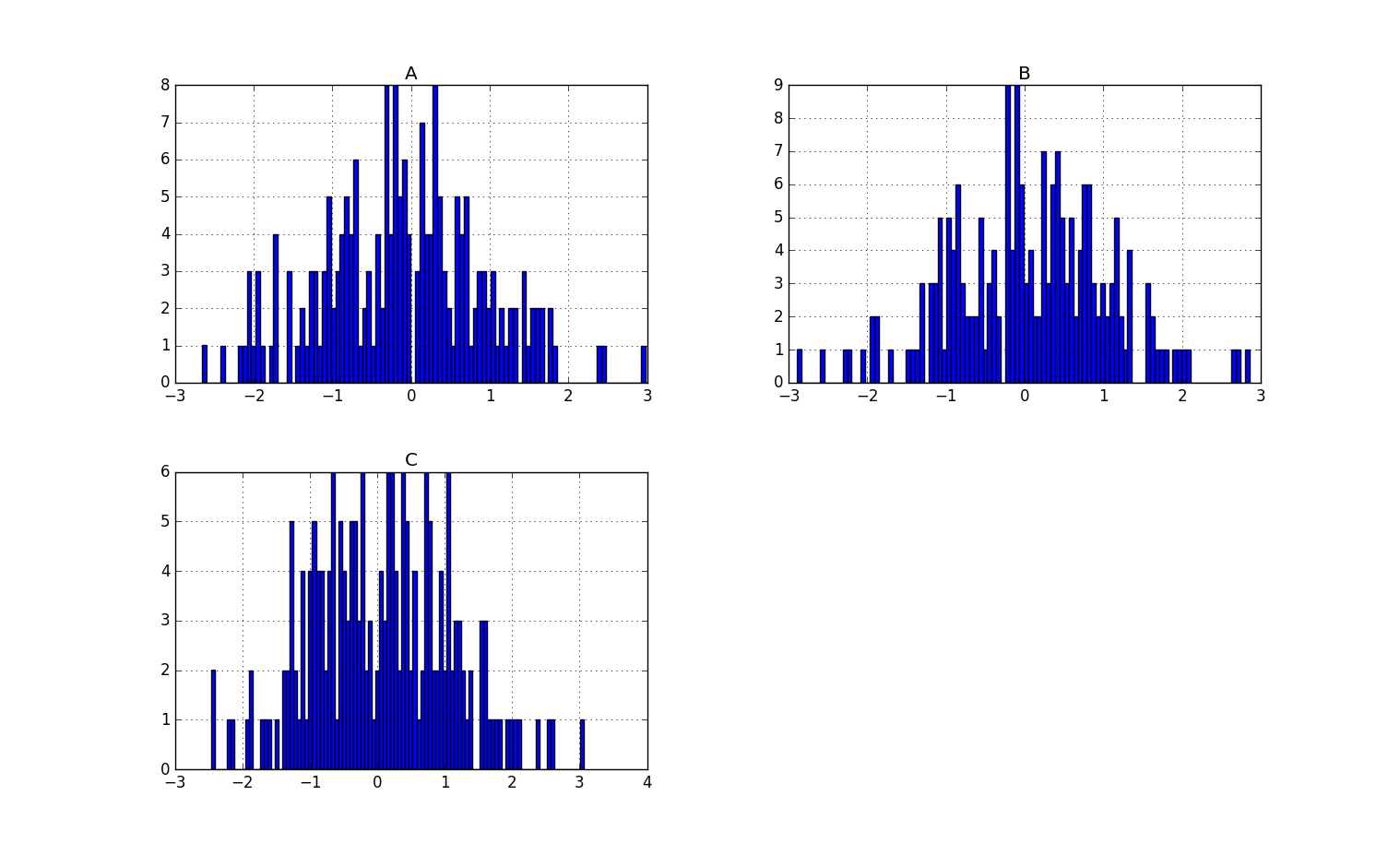
plt调用hist函数。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
#print v
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])

ind = np.linspace(-2.5, 2.5, 200)
print len(df["A"]), len(ind)
plt.hist(df["A"], ind, alpha = 0.5, label = "x", color = "r")

plt.legend(loc = "upper left")
plt.show()
plt.hist(df["B"], ind, alpha = 0.5, label = "y", color = "g")
plt.legend(loc = "upper left")
plt.show()
plt.hist(df["C"], ind, alpha = 0.5, label = "z", color = "b")
plt.legend(loc = "upper left")
plt.show()

执行结果：

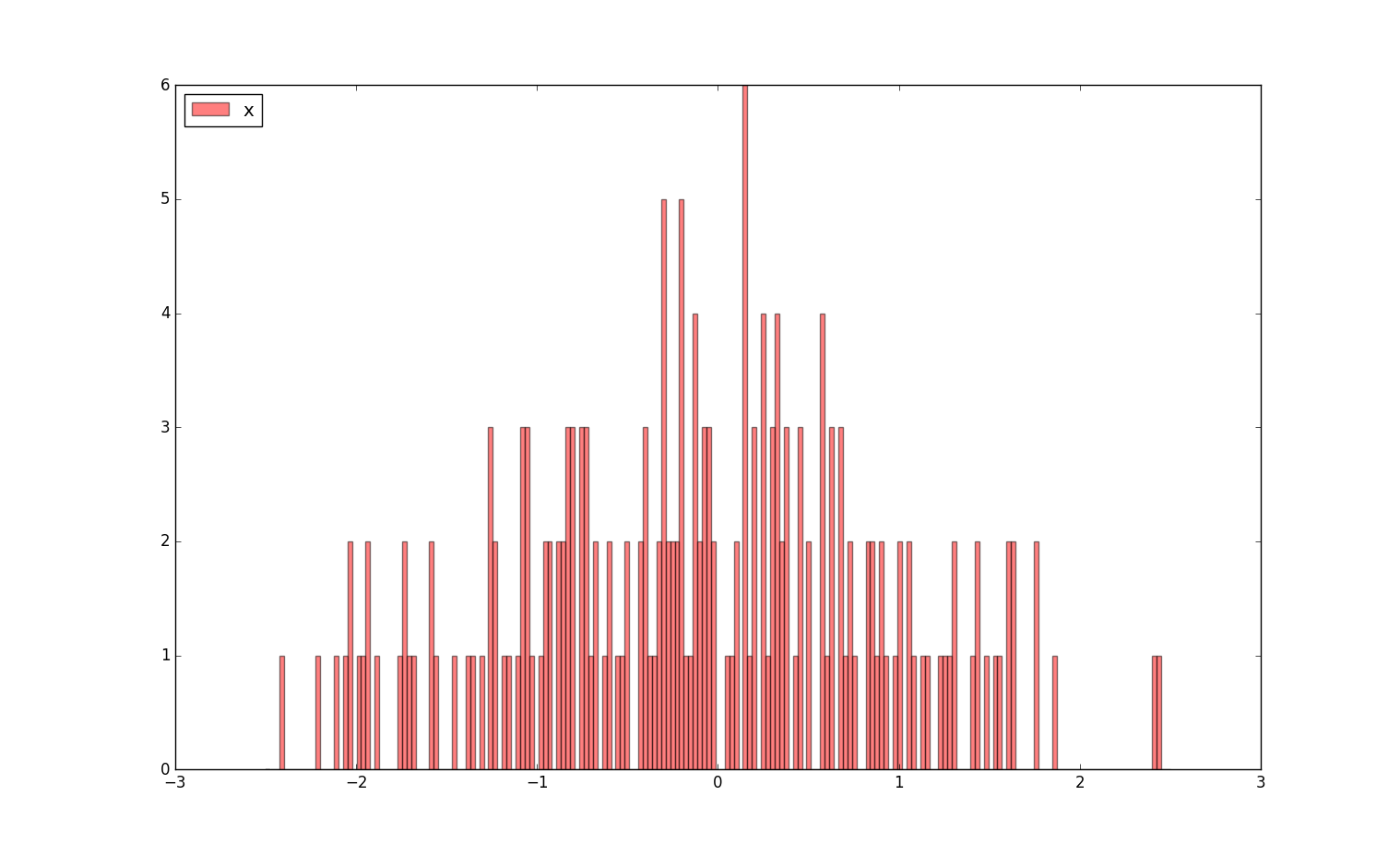
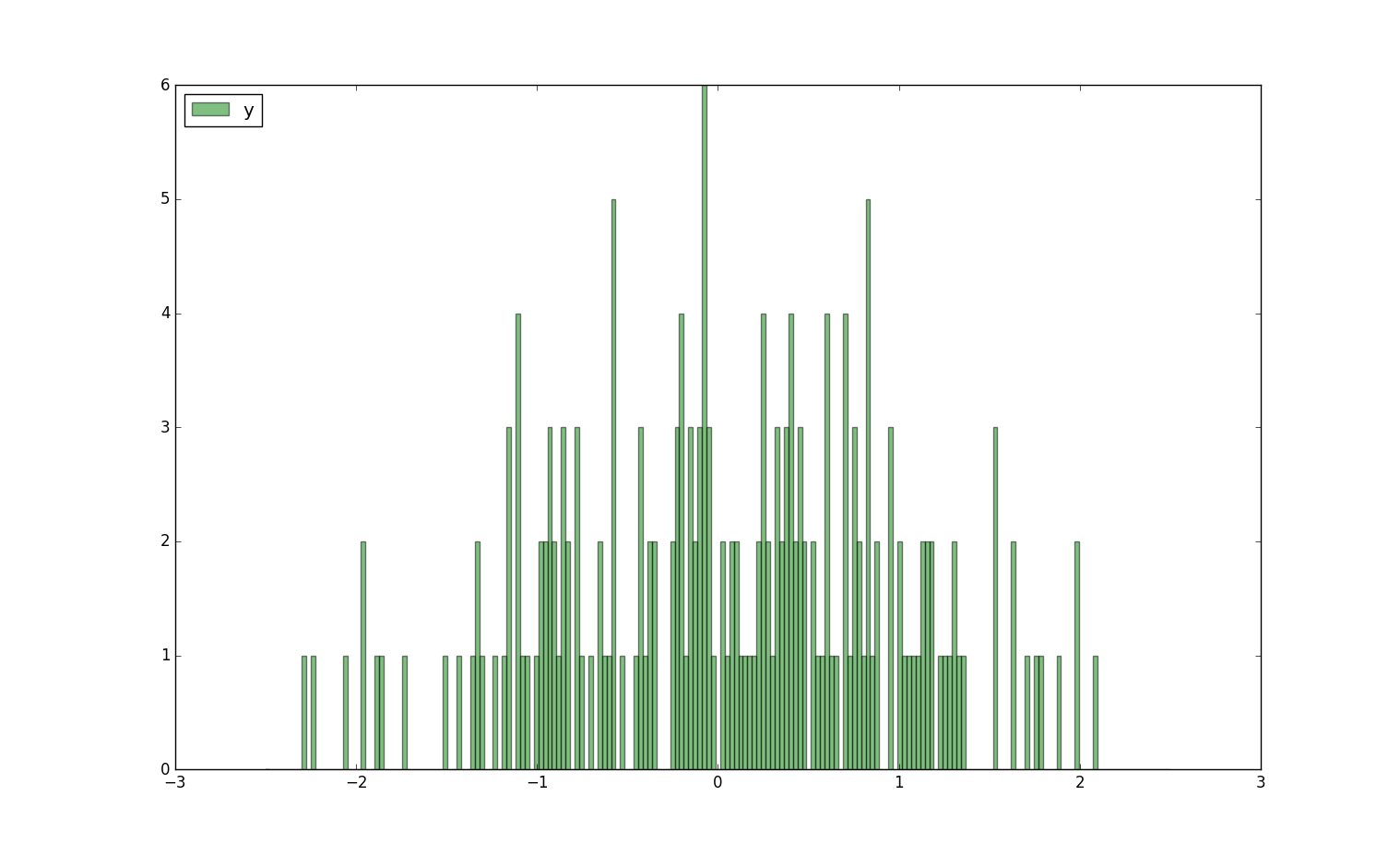
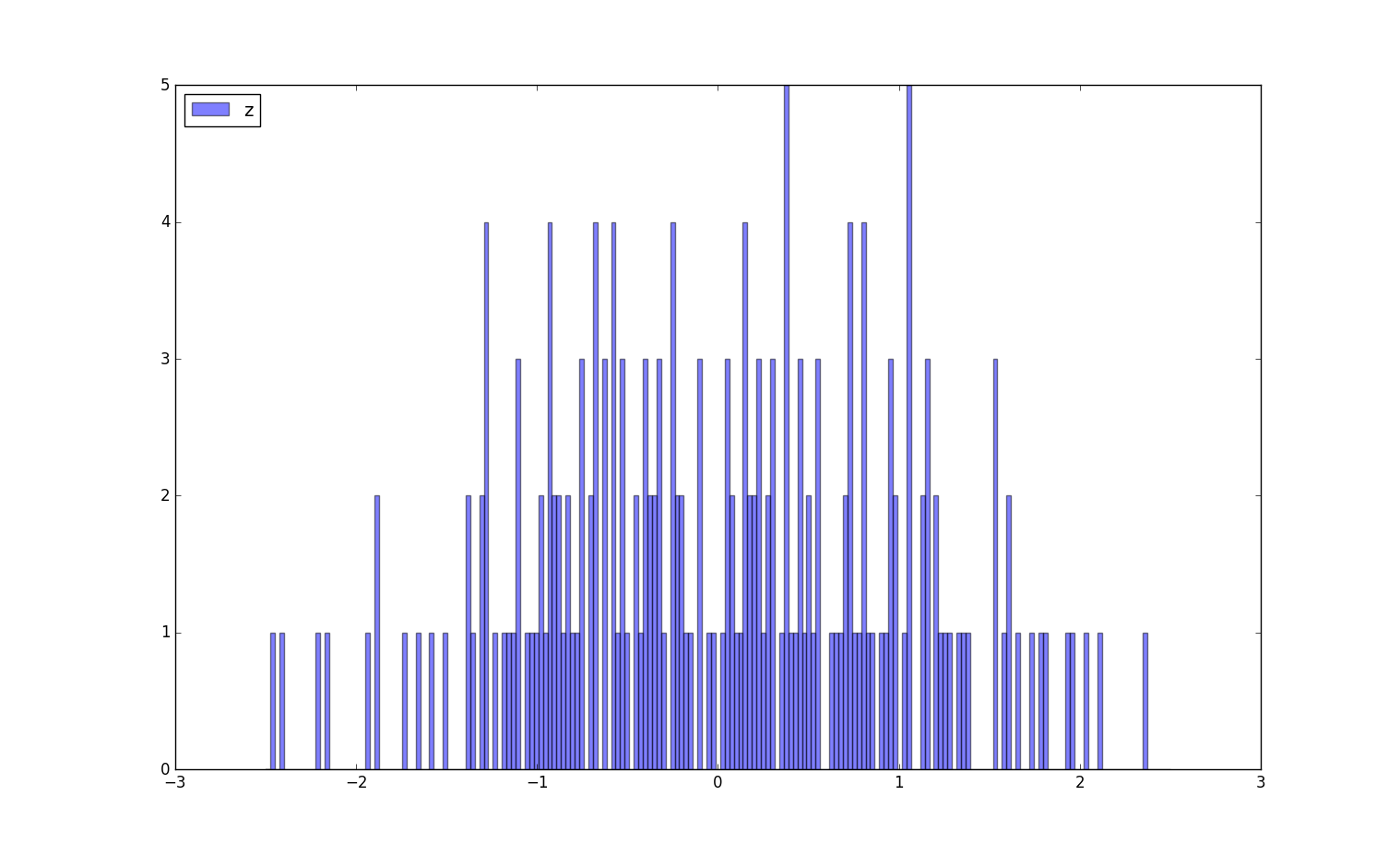
43.3 茎叶统计图

在pandas里可以使用boxplot来绘制统计学里的茎叶统计图。它由五个数值点组成：最小值(min)，下四分位数(Q1)25%，中位数(median)50%，上四分位数(Q3)75%，最大值(max)。也可以往盒图里面加入平均值(mean)，上四分位数到最大值之间建立一条延伸线，这个延伸线成为“胡须(whisker)”。在分析数据的时候，盒图能够有效地帮助我们识别数据的特征：

直观地识别数据集中的异常值(查看离群点)。
判断数据集的数据离散程度和偏向(观察盒子的长度，上下隔间的形状，以及胡须的长度)。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
dfc.boxplot()
plt.show()

结果如下：

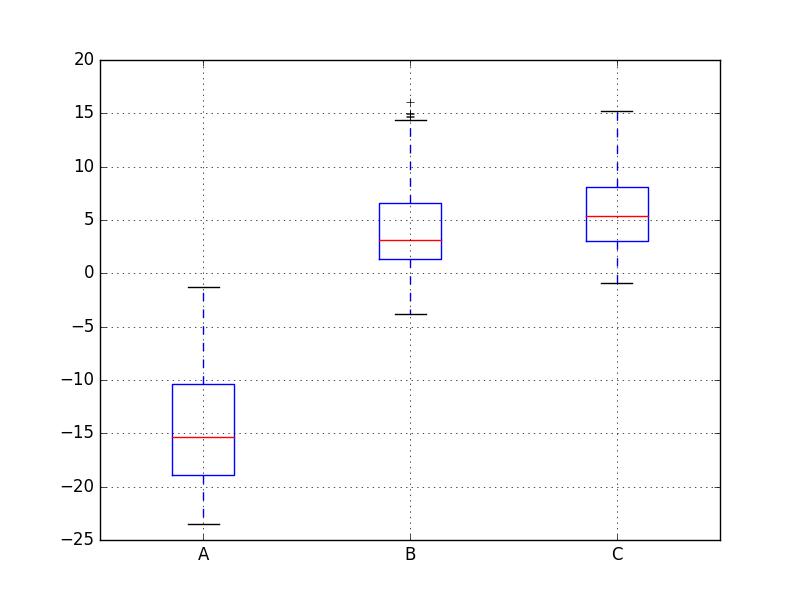
程序对A、B、C三列分别绘制了可视化的茎叶统计图。

43.4 面积图(区域图)Area Plot

可以通过pandas的plot指定kind为area来绘制统计面积图。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
dfc.plot(kind= "area", stacked = False)
plt.show()
dfc.plot.area(stacked = False)
plt.show()

执行结果：

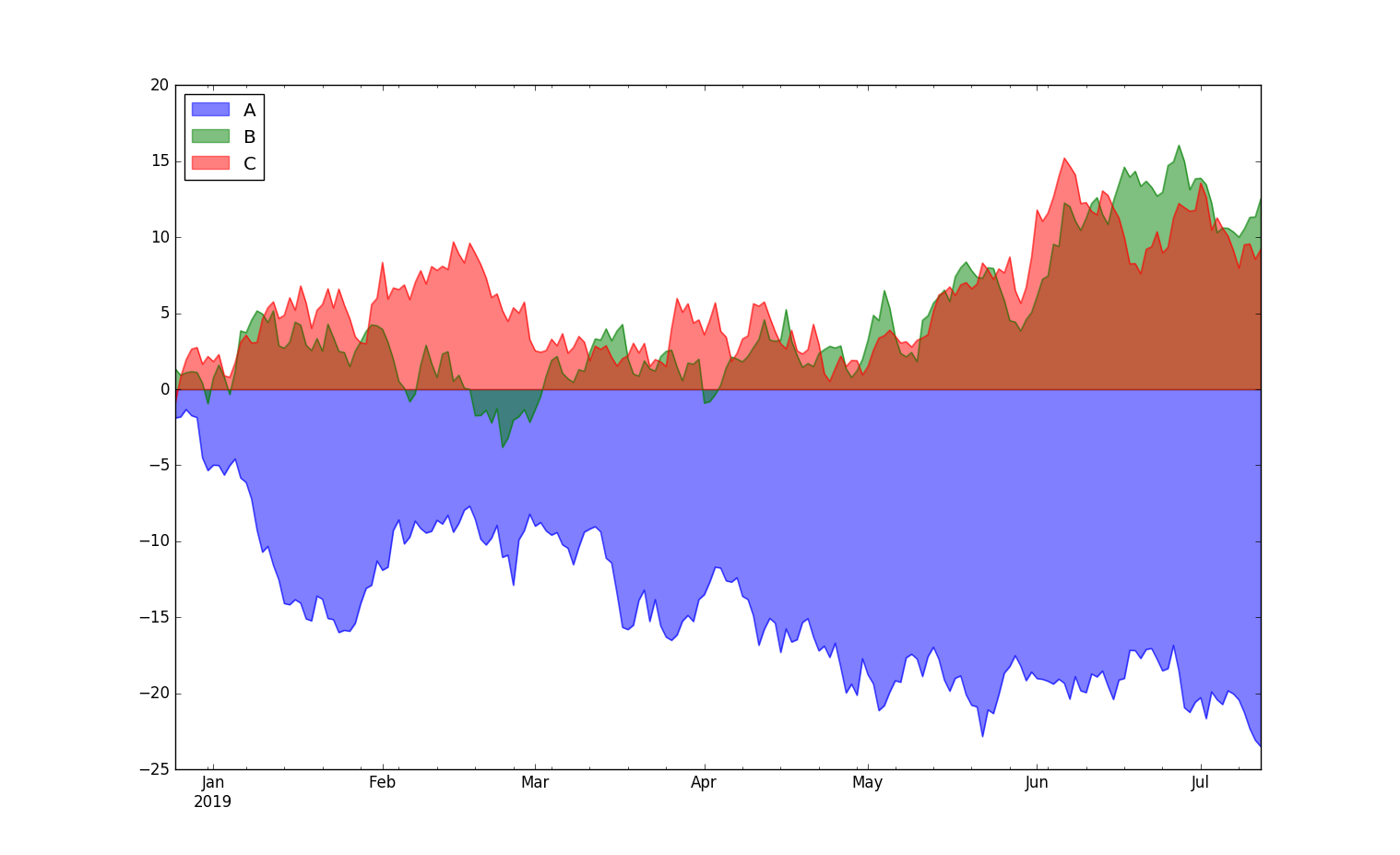
43.4 散点图scatter

scatter函数可以绘制两个变量间的关系即散点图表示因变量随自变量而变化的大致趋势。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
plt.scatter(x = df["A"], y = ind)
plt.show()

执行结果：

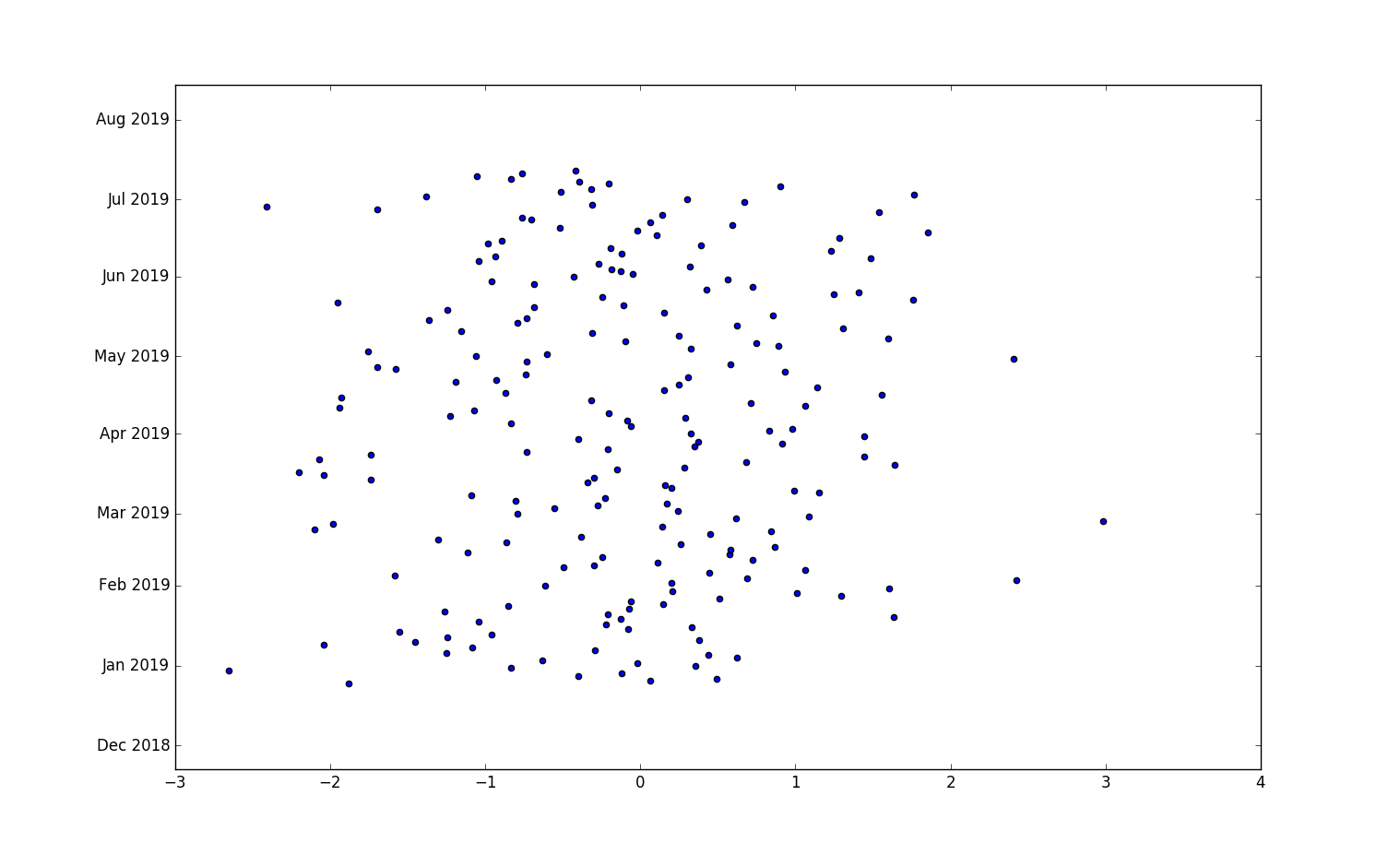
43.5 核估计图

对于大量一维数据的可视化，除了使用直方图histogram，还有一种更好的方法：核密度估计(Kernel Density Estimates，简称KDE)。所谓核密度估计，就是采用平滑的峰值函数(“核”)来拟合观察到的数据点，从而对真实的概率分布曲线进行模拟。核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估计方法。理论上，所有平滑的峰值函数均可作为KDE的核函数来使用，只要对归一化后的KDE而言(描绘在图上的是数据点出现的概率值)，该函数曲线下方的面积和等于1即可 — 只有一个数据点时，单个波峰下方的面积为1，存在多个数据点时，所有波峰下方的面积之和为1。概而言之，函数曲线需囊括所有可能出现的数据值的情况。常用的核函数有：矩形、Epanechnikov曲线、高斯曲线等。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(111111)
v = np.random.randn(200, 3)
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
print dfc
dfc["A"].hist(normed = True)
dfc["A"].plot(kind = "kde")
dfc["B"].hist(normed = True)
dfc["B"].plot(kind = "kde")
dfc["C"].hist(normed = True)
dfc["C"].plot(kind = "kde")
plt.show()

执行结果:

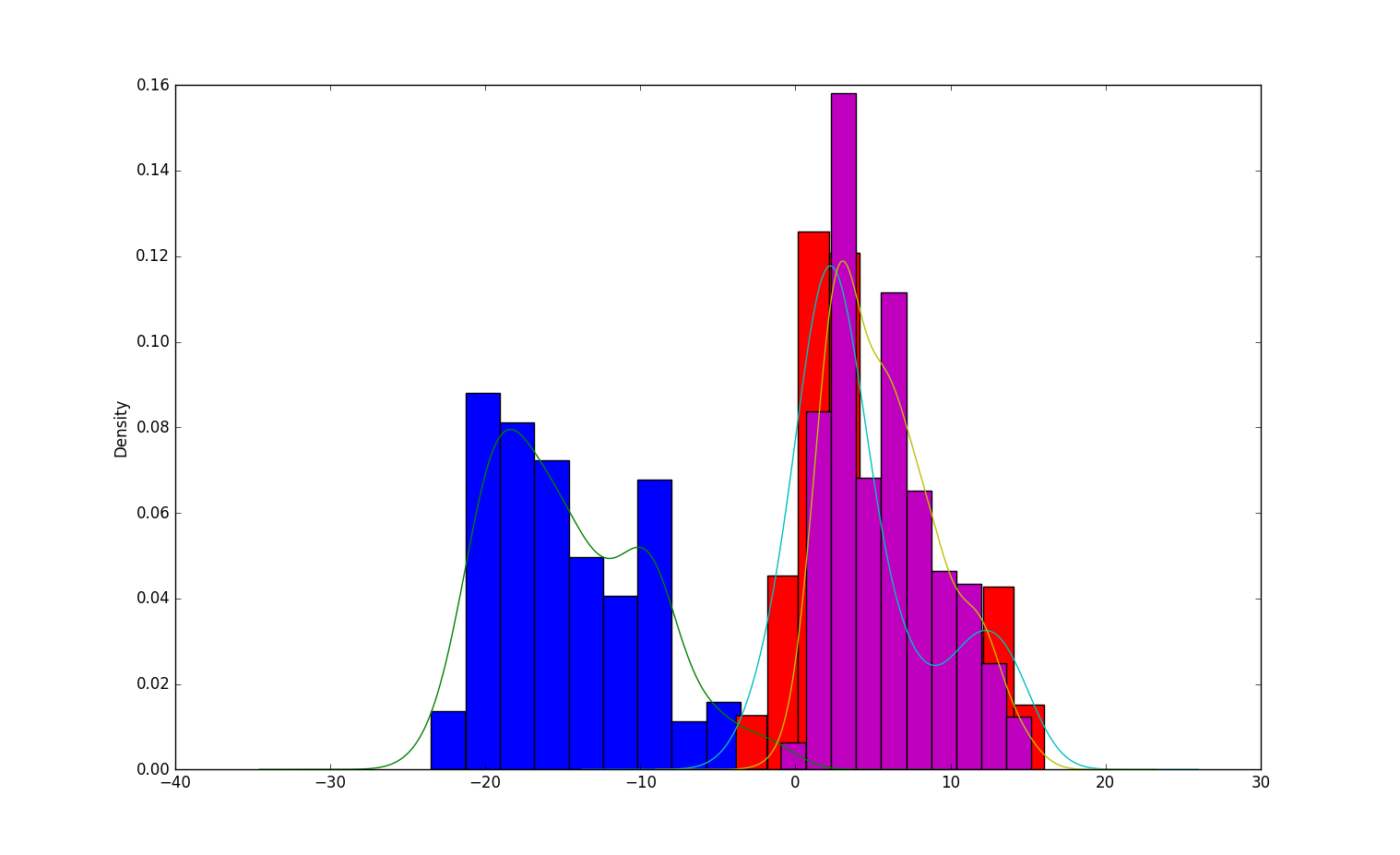
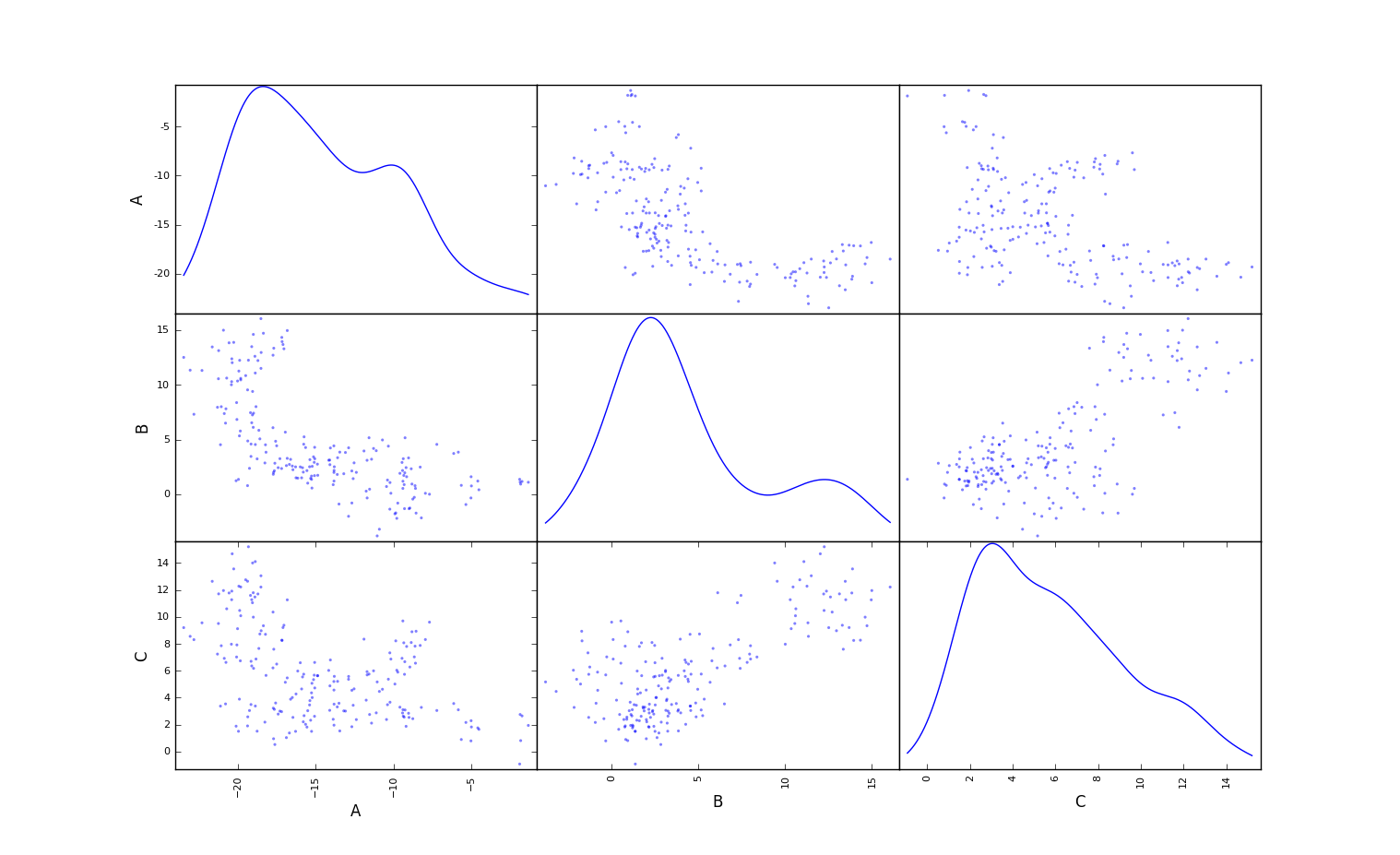
43.6 散点矩阵图

将高维度的数据每两个变量组成一个散点图，再将他们按照一定的顺序组成散点图矩阵。通过这样的可视化方式，能够将高维度数据中所有的变量两两之间的关系展示出来。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas.plotting import scatter_matrix
np.random.seed(111111)
v = np.random.randn(200, 3)
ind = pd.date_range('2018-12-25', periods = 200)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
scatter_matrix(dfc, diagonal = "kde")
plt.show()

执行结果：

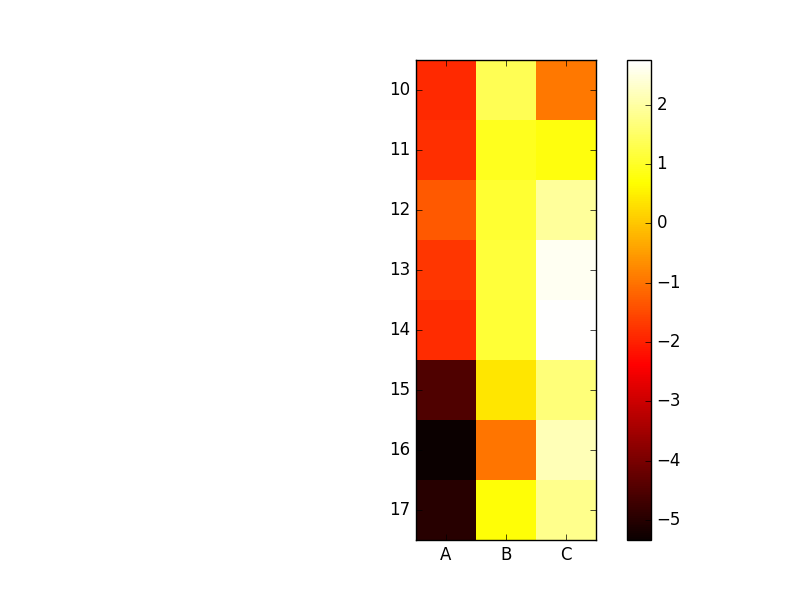
43.7 热力图heatmap

热力图这个名字可能听起来很高大上，但是实际上它等同于我们常说的密度图。利用热力图可以看数据里多个特征量两两间的相似度。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
np.random.seed(111111)
v = np.random.randn(8, 3)
#ind = pd.date_range('2018-12-25', periods = 8)
ind = range(10,18)
df = pd.DataFrame(v, index = ind, columns = ["A", "B", "C"])
dfc = df.cumsum()
plt.imshow(dfc, cmap = "hot", interpolation = "none")
plt.colorbar()
plt.xticks(range(len(dfc.columns)), dfc.columns)
plt.yticks(range(len(dfc)), dfc.index)
plt.show()

执行结果：

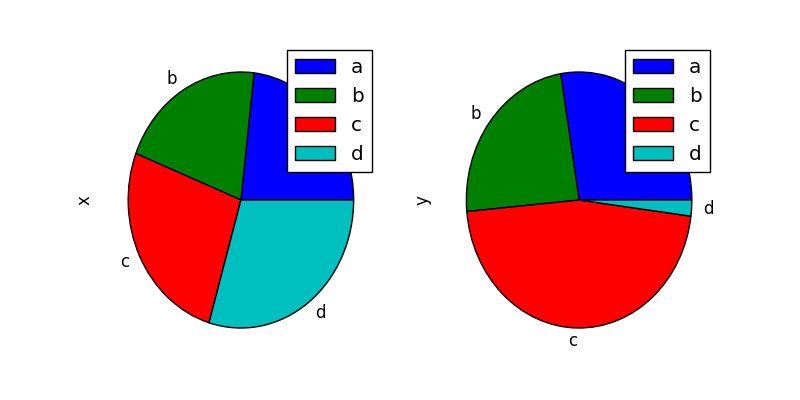
43.8 饼图

无需解释。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
df = pd.DataFrame(3 * np.random.rand(4, 2), index=['a', 'b', 'c', 'd'], columns=['x', 'y'])
df.plot(kind='pie', subplots=True, figsize=(8, 4))
plt.show()

执行结果：