6. SciPy之svd典型应用

上一章就scipy的方程求解介绍了很多的分解，通过分解求值变得比较简单，最后介绍了一下svd分解的基本使用，本章就svd的应用举两个例子：图像压缩和信号去噪，展示一下svd的现实应用。

6.1 svd实现图像的压缩的原理

任意形状的矩阵$A$经过svd分解会得到$U$，$\Sigma$，$V^T$（V的转置）三个矩阵，其中$U$是一个$M\times M$的方阵，被称为左奇异向量，方阵里面的向量是正交的；$\Sigma$是一个$M\times N$的对角矩阵，除了对角线的元素其他都是0，对角线上的值称为奇异值；$V^T$(V的转置)是一个$N \times N$的矩阵，被称为右奇异向量，方阵里面的向量也都是正交的。

$$ A_{m \times n} = U_{m \times m}\Sigma_{m \times n}V_{n \times n}^T $$ 可以计算$\Sigma$前x个奇异值的平方和占所有奇异值的平方和的比例，如果大于90%，我们就选这x个奇异值重构矩阵（剩余的数据代表的可能是噪声，无用数据）。 $$ x = \frac{\sum_{i=1}^{x}\sigma_i^2}{\sum_{i=1}^{n}\sigma_i^2} > 90\% $$ 那么重构的A'为： $$ A_{m \times n} = U_{m \times m}\Sigma_{m \times n}V_{n \times n}^T \approx U_{m \times x}\Sigma_{x \times x}V_{x \times n}^T $$ 以上的理论用代码表示如下：

#coding:utf-8
from scipy.linalg import svd
import matplotlib.pyplot as plt
import numpy as np
import numpy
a = [[0, 0, 0, 2, 2],
    [0, 0, 0, 3, 3],
    [0, 0, 0, 1, 1],
    [1, 1, 1, 0, 0],
    [2, 2, 2, 0, 0],
    [5, 5, 5, 0, 0],
    [1, 1, 1, 0, 0]]
A = np.array(a)
print A
U, s, Vh = svd(A)
print s.shape,s
# 选x
for i in range(s.shape[0]):
    percent = np.sum(np.square(s[:i+1])) * 1.0 / np.sum(np.square(s))
    if percent >= 0.9:
        print "x", i + 1
        break
# 重构A
for i in range(1, s.shape[0]):
    A = numpy.dot(U[:,0:i],numpy.dot(numpy.diag(s[0:i]),Vh[0:i,:]))
    print np.array(A, dtype=np.uint8),"#:", i

程序执行结果：

[[0 0 0 2 2]
 [0 0 0 3 3]
 [0 0 0 1 1]
 [1 1 1 0 0]
 [2 2 2 0 0]
 [5 5 5 0 0]
 [1 1 1 0 0]]
(5,) [  9.64365076e+00   5.29150262e+00   8.36478329e-16   6.91811207e-17
   3.04963694e-34]
x 2
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [1 0 1 0 0]
 [2 1 2 0 0]
 [5 4 5 0 0]
 [1 0 1 0 0]] #: 1
[[0 0 0 1 1]
 [0 0 0 2 2]
 [0 0 0 1 1]
 [1 0 1 0 0]
 [2 1 2 0 0]
 [5 4 5 0 0]
 [1 0 1 0 0]] #: 2
[[0 0 0 1 1]
 [0 0 0 2 2]
 [0 0 0 1 1]
 [1 0 1 0 0]
 [2 1 2 0 0]
 [5 4 5 0 0]
 [1 0 1 0 0]] #: 3
[[0 0 0 1 1]
 [0 0 0 2 2]
 [0 0 0 1 1]
 [1 0 1 0 0]
 [2 1 2 0 0]
 [5 4 5 0 0]
 [1 0 1 0 0]] #: 4

从选择x那段代码的执行结果可以看出A矩阵svd分解出来的s前2个奇异特征值平方和大于总奇异值平和的90%。从重构A下面的代码可以看出x = 2 的重构矩阵已经非常接近A矩阵了，可以发现原始数据中非零的部分都完整的保存了下来，说明选择的奇异值几乎能较完整地保存了所有有用信息。

6.2 svd实现对图像的压缩

有了上边的理论基础，接下来可以用一副具体的图来展示一下svd实现对图像的压缩。

import scipy.misc
from scipy.linalg import svd
import matplotlib.pyplot as plt
import numpy as np
import numpy
img = scipy.misc.face()[:,:,0]

print img.shape,type(img)
img = np.matrix(img)
U,s,Vh=svd(img)
plt.gray()

plt.subplot(221,aspect='equal')
plt.title("orignal")
plt.imshow(img)
plt.imsave('org.png', img)

A = numpy.dot(U[:,0:10],numpy.dot(numpy.diag(s[0:10]),Vh[0:10,:]))
plt.subplot(222,aspect='equal')
plt.title(":10")
plt.imshow(A)
plt.imsave('a10.png', A)

A = numpy.dot(U[:,0:50],numpy.dot(numpy.diag(s[0:50]),Vh[0:50,:]))
plt.subplot(223,aspect='equal')
plt.title(":50")
plt.imshow(A)
plt.imsave('a50.png', A)

A = numpy.dot(U[:,0:100],numpy.dot(numpy.diag(s[0:100]),Vh[0:100,:]))
plt.subplot(224,aspect='equal')
plt.title(":100")
plt.imshow(A)
plt.imsave('a100.png', A)

plt.show()

程序执行结果：

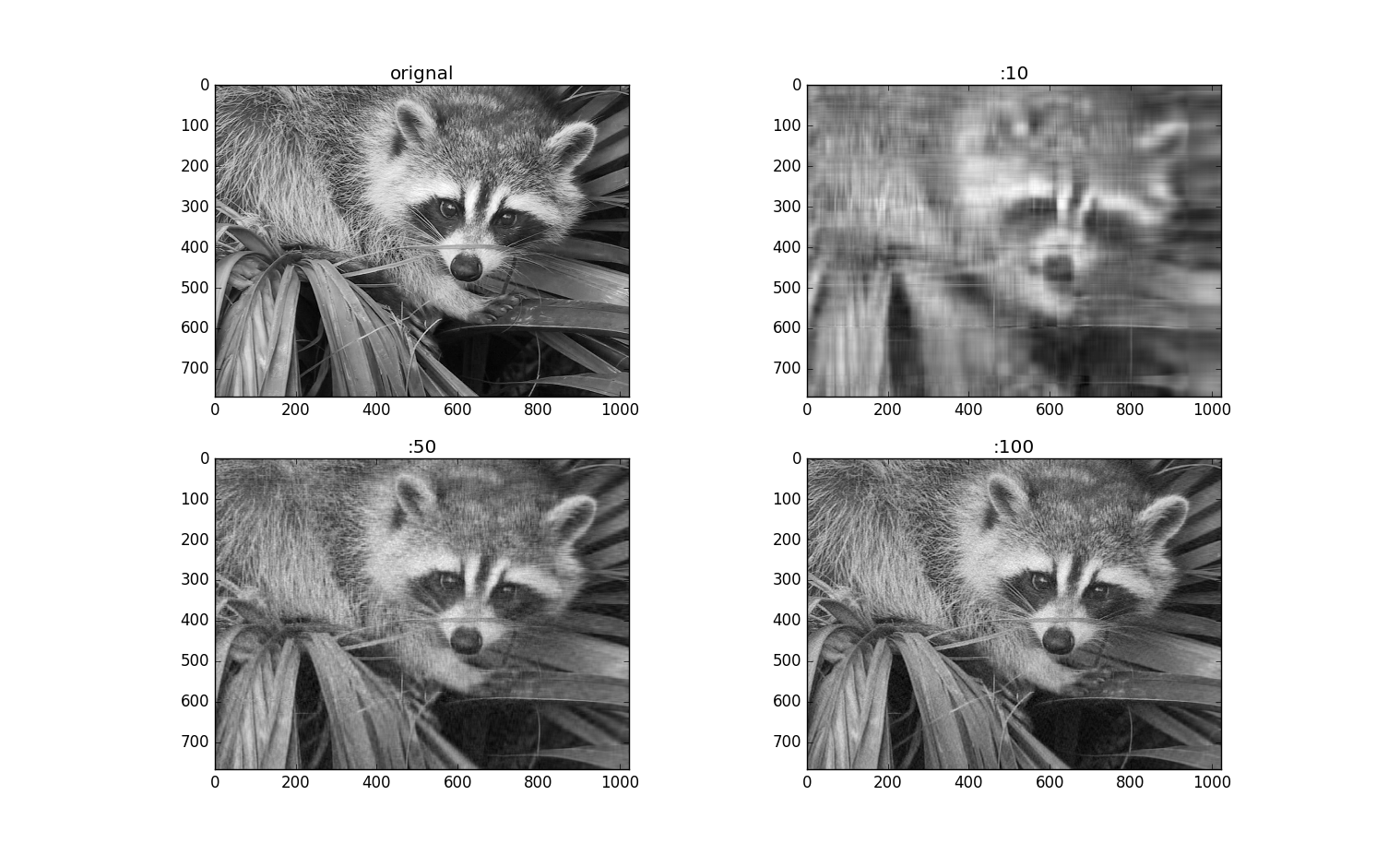
从上图可以看出选不同的奇异值个数得到的图像的清晰度是变化的。第一副图是原图的黑白显示，第2、3、4分别取了10、50、100个奇异值后重构了图像A。下图的各个图像文件的大小。

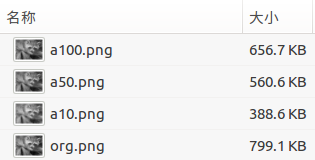
说明选取奇异值的个数的不同，重构的图像文件大小不同，清晰度不同，正确的选择x决定图像的质量。

6.3 svd实现信号去噪

本例子先做一个sin函数的数据集a，a是由标准正弦波numpy.sin()加上噪声ss = np.random.normal(mu, sigma, 400)后形变(reshape)成一个矩阵而最终构成的a = (np.sin(x) + ss).reshape(20, 20)。接下来就是调用scipy.linalg模块下的svd对a进行svd分解U,s,Vh = svd(a)，得到U,s,Vh三个值。 s是奇异值主对角非0的对角阵，记录着各个奇异值，选择不同个数的奇异值A = numpy.dot(U[:,0:2],numpy.dot(numpy.diag(s[0:2]),Vh[0:2,:]))和A = numpy.dot(U[:,0:1],numpy.dot(numpy.diag(s[0:1]),Vh[0:1,:]))可以重构矩阵a为A，从而实现信号去噪处理。

import matplotlib.pylab as plt
import numpy as np
import numpy
from scipy.linalg import svd
x = np.linspace(-np.pi, np.pi, 400)
mu, sigma = 0, 0.05
ss = np.random.normal(mu, sigma, 400)
a = (np.sin(x) + ss).reshape(20, 20)

U,s,Vh = svd(a)
print s
A = numpy.dot(U[:,0:2],numpy.dot(numpy.diag(s[0:2]),Vh[0:2,:]))
aa = A.reshape((400,))

plt.subplot(221,aspect='equal')
plt.plot(x, np.sin(x))
plt.title("sin")

plt.subplot(222,aspect='equal')
plt.plot(x, np.sin(x) + ss)
plt.title("sin with noise")

plt.subplot(223,aspect='equal')
plt.title("sin remove noise x = 2")
plt.plot(x, aa)

A = numpy.dot(U[:,0:1],numpy.dot(numpy.diag(s[0:1]),Vh[0:1,:]))
aa = A.reshape((400,))
plt.subplot(224,aspect='equal')
plt.title("sin remove noise x = 1")
plt.plot(x, aa)

plt.show()

程序执行结果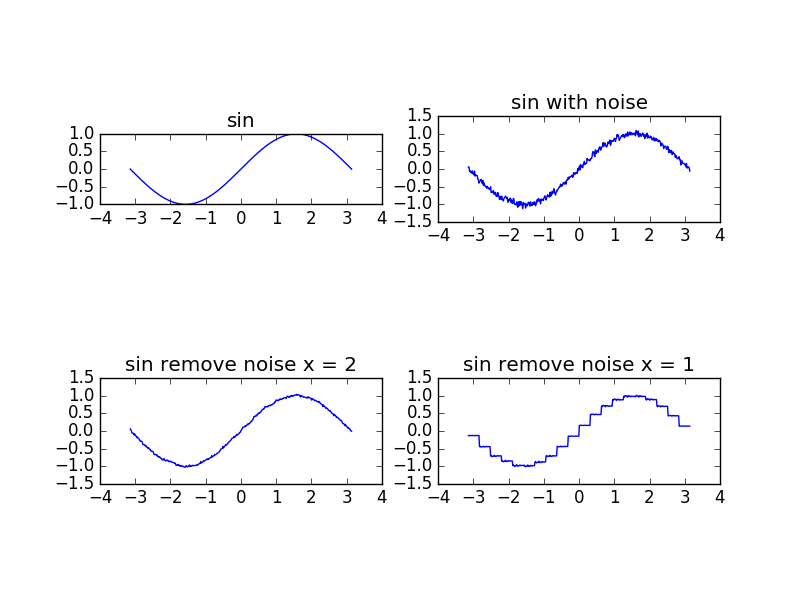：第一副图是纯sin波形，第2副图是加了噪声的波形，第三副选择2个奇异值重构A结果很接近标准sin波形实现了去噪，第四副图是选了1个奇异值重构A的结果。

6.4 总结

svd分解在机器学习和深度学习以及计算机视觉等领域都有很多涉及，需明白基础不牢靠，学习机器学习也就是浮于表面。