7. Scipy Tutorial-最小二乘法拟合

scipy.optimize包里提供了最小二乘法的功能函数leastsq，最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 $$ J(\theta) = \min\sum_{i = 1}^m (f(x_i) - y_i)^2 $$ 这里的$f(x_i) = a_0 + a_1x^1+a_2x^2+\dots+a^nx^n$为要找出来的函数模型，$a_0,\cdots,a_n$为要确定的参数，$y_i$为给出的测试数据，依据这些数据$y_i$通过最小化误差的平方和$J(\theta)$来寻找最佳的匹配函数，确定$f(x)$函数里的$a_0,\cdots,a_n$，找到一个合适的函数来“包容”下这些数据,即拟合。 用leastsq来求$f(x)$里的参数$a_0,\cdots,a_n$，，需要定一个一个求$J(\theta)$的差值平方的函数，然后把这个函数传给leastsq函数里找$f(x)$里的参数。

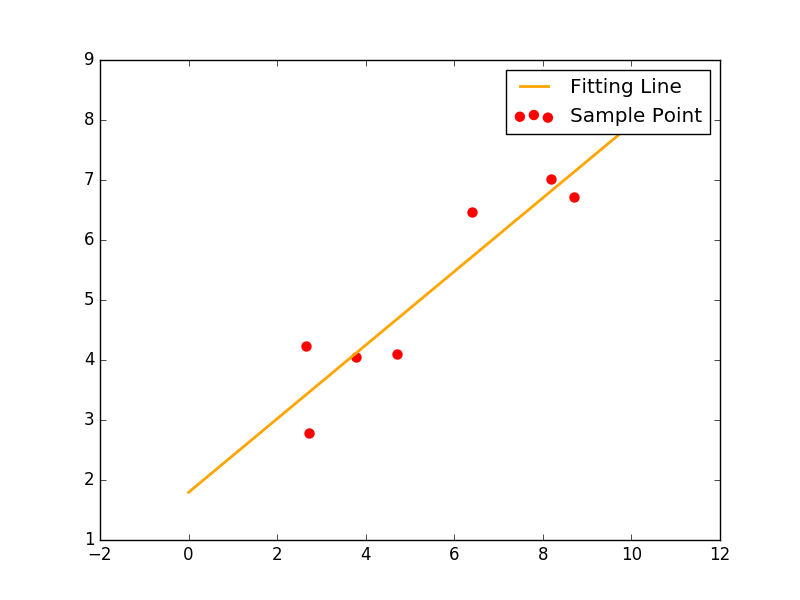
• 线性拟合，假设数据具有线性的趋势，那么$f(x) = a x + b$需要通过最小二乘法找到的一个合适的a和b这样的一条直线来拟合所有数据。

import numpy as np
from scipy.optimize import leastsq
def err(p, x, y):
    return p[0] * x + p[1] - y
p0 = [100, 20]
Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
ret = leastsq(err, p0, args = (Xi, Yi))
print ret 
import matplotlib.pyplot as plt
k, b = ret[0]
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3)
x = np.linspace(0,10,1000)
y = k * x + b
plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2)
plt.legend()
plt.show()  

执行结果：

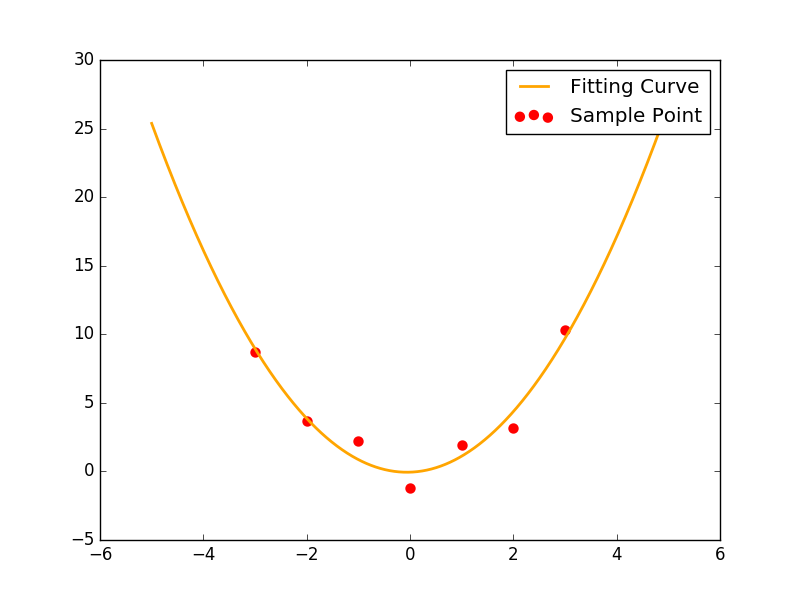
• 二次拟合，如果数据具有二次多项式的特征可以用$f(x) = a x^2 + bx + c$来拟合。

#coding:utf-8
import numpy as np
from scipy.optimize import leastsq
Xi=np.array([0,1,2,3,-1,-2,-3])
Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])
def error(p,x,y):
    return p[0]*x**2+p[1]*x+p[2]-y 
p0 = [5,2,10]
ret = leastsq(error,p0,args=(Xi,Yi))
a,b,c= ret[0]
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3)
x = np.linspace(-5,5,1000)
y = a * x ** 2 + b * x + c
plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2)
plt.legend()
plt.show()

执行结果：