20. Scipy Tutorial-图像卷积convolve
上一章用convolve函数简要介绍了一下离散数据的卷积,图像在计算机里以二维矩阵的形式存储,也算是离散的数据,所以卷积在图像方面的应用很多,CNN等深度学习里就大量涉及到卷积的问题。 图像的卷积有三种模式:full、same和valid本章就这三种模式进行讨论(这里假设移动步长stride = 1)。这三种模式实际是在核k对输入数据i滑动卷积过程中有重叠但有的时候不是全部重叠在一起,核k可能有一部分和输入数据重合而另一部分漂在输入数据外部,技术上对漂在外部的处理方式是填零Zero padding。分别设定输入数据的列数为i、核的列数为k,而每边填0列数为p,卷积的列数为o。
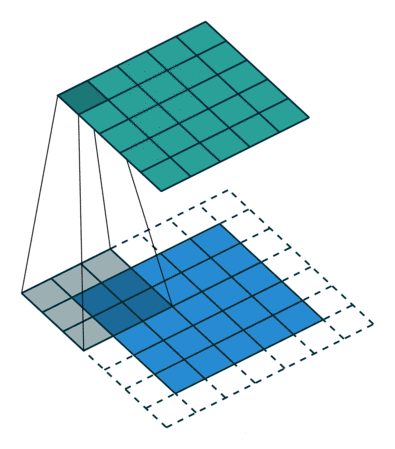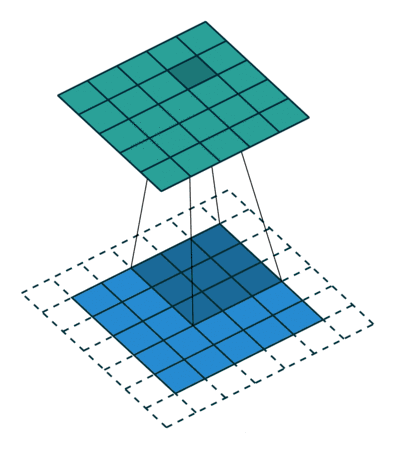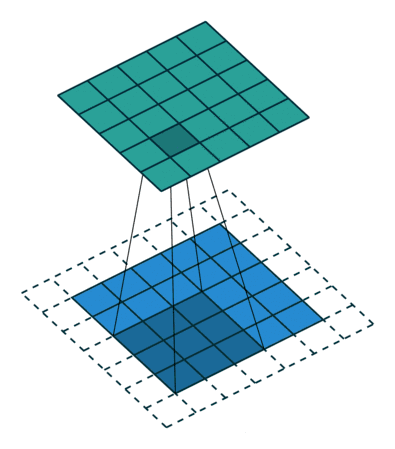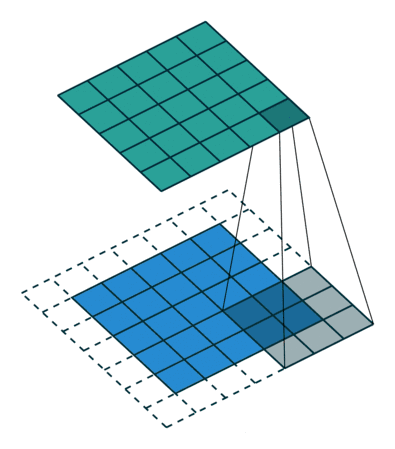
20.1 Full padding模式
full模式卷积,默认的scipy.signal里的convolve函数的模式就是使用的full模式。full的意思$i$和$k$只要有重叠$p = k - 1$,即开始卷积,所以会出现下图最左上角、右下角的情况,full模式卷积结果会将$i$增大的尺寸变成$o$。步长为1,输入数据(图片)尺寸大小为$i\times i$,卷积核大小为$k\times k$,卷积后图像(列)大小: $$ o = (i - k +2p + 1) \times (i - k +2p + 1) $$
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
x = np.array([[1.0, 1.0, 0.0],[1.0, 1.0, 0.0], [0.0, 0.0, 0.0]])
h = np.array([[1.0, 0.0], [0.0, 1.0]])
y = signal.convolve(x, h, mode = "full")
print y
执行结果:
[[1. 1. 0. 0.]
[1. 2. 1. 0.]
[0. 1. 1. 0.]
[0. 0. 0. 0.]]
这里需提醒一下:$h$旋转$180^{\circ}$(参看前一章)后的$h'$和$h$一样。

(1). 网上前辈做了一个很好的动图展示出了full模式的卷积的动态过程($2\times 2$的为被卷积的数据x,$3\times 3$的为核h,最上边的$4\times 4$的为卷积结果y):
动图对$2\times2$的矩阵数据(例如:$x$)进行核为$3\times3$(例如:$h$)的卷积,得到$4 \times 4$的卷积结果($y$)。动图里的$i = 2, k = 3, p = 2$则卷积结果有: $$ o = 2 - 3 + 4 + 1 = 4 $$ 列即$4 \times 4$的卷积结果。
(2). 另一尺寸的full模式卷积:
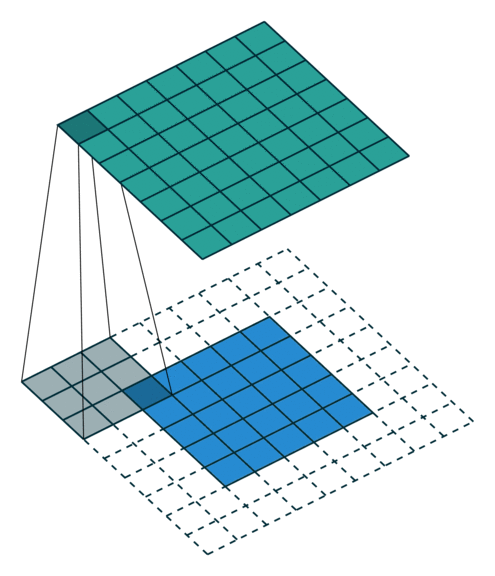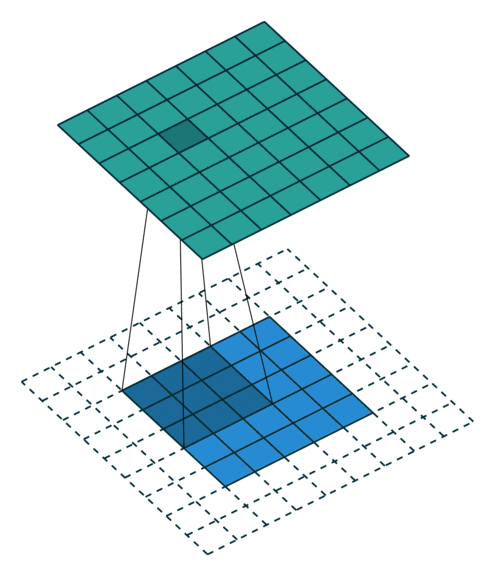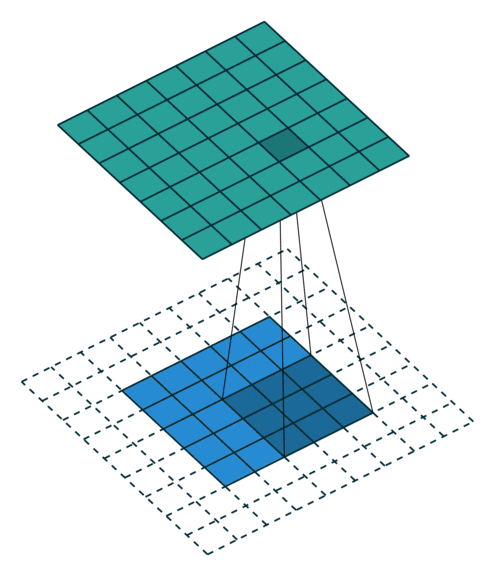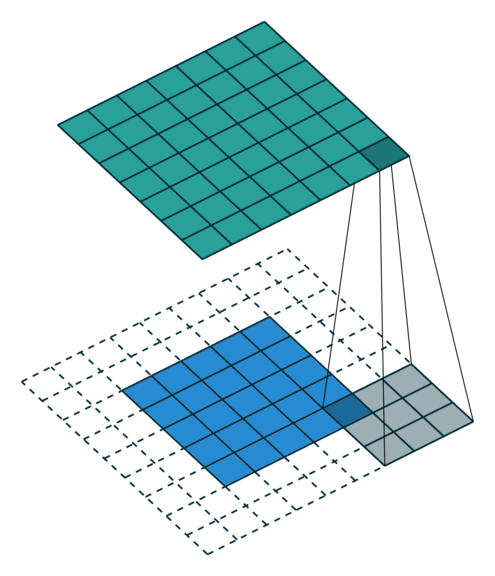
动图的输入数据的列数$i = 5$、核的列数$k = 3$、每边最大填0列数$p = 2$,那么卷积结果的列数为$o = i - k + 2p + 1 = 5 -3 + 4 + 1 = 7$。
20.2 No zero padding模式
valid模式卷积,又称No zero padding即只在被卷积的x的内部滑动卷积。valid 操作,滑动步长为S为1(本章的卷积函数没有步长的参数,故令S=1),输入数据(例如图片)大小为$i\times i$,卷积核k大小为$k\times k$,那么外部不填充0,则$p = 0$,卷积后图像大小: $$ o = i - k + 1 $$
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
x = np.array([[1.0, 1.0, 0.0],[1.0, 1.0, 0.0], [0.0, 0.0, 0.0]])
h = np.array([[1.0, 0.0], [0.0, 1.0]])
y = signal.convolve(x, h, mode = "valid")
print y
执行结果:
[[2. 1.]
[1. 1.]]
例子里的input为$3\times3$则$i = 3$,kernel核为$2\times2$则有$k = 2$,步长为1,非填0卷积有$p = 0$则卷积的output结果的尺寸为:
$$ o = i - k + 1 = 3 -2 + 1 = 2 $$

也就是说核$h$在数据$x$的内部滑动。
(1). 网上经典动图,如下所示(最下面的是x,移动的是h,上边的是y即卷积结果)。
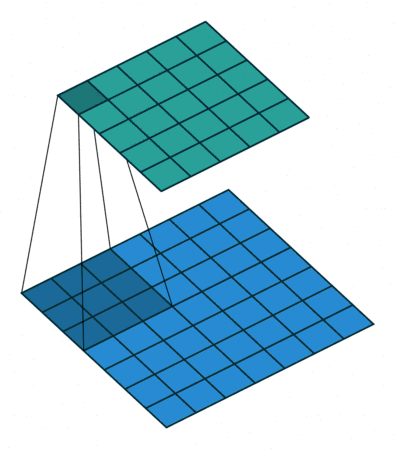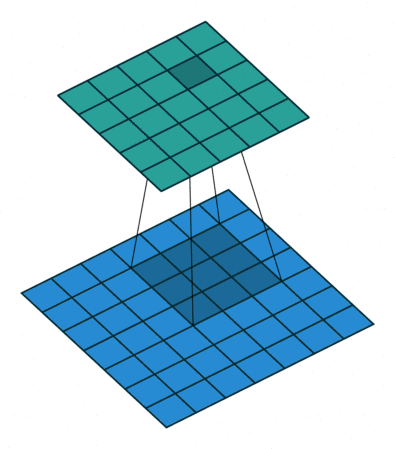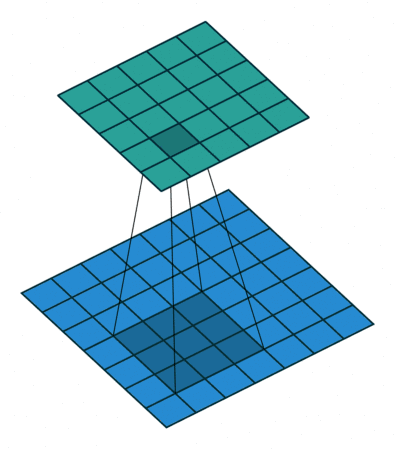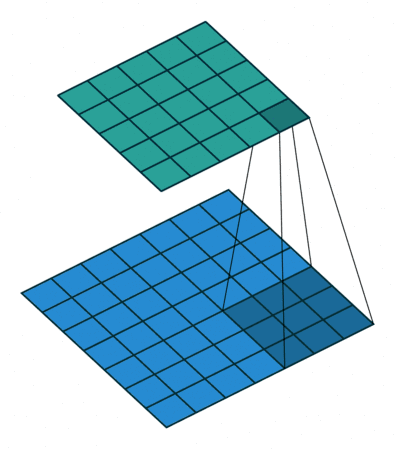
上边动图$i = 7, k = 3, p = 0$则卷积结果的列数$o = i - k + 1 = 7 - 3 + 1 = 5$。
(2). 还有一个动图也不错!

上边动图$i =4, k =3, p = 0$则卷积结果的列数$o = i - k + 1 = 4 - 3 + 1 = 2$。
(3).还有一个二维的动图:
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
i = np.array([[1,1,1,0,0],
[0,1,1,1,0],
[0,0,1,1,1],
[0,0,1,1,0],
[0,1,1,0,0]])
k = np.array([[1,0,1],
[0,1,0],
[1,0,1]])
o = signal.convolve(i, k, mode = "valid")
print o
程序执行结果:
[[4 3 4]
[2 4 3]
[2 3 4]]
这里需要注意$k$旋转$180^{\circ}$后的$k'$,和$k$一模一样,千万不要认为下图滑动的就是$k$,是$k'$。
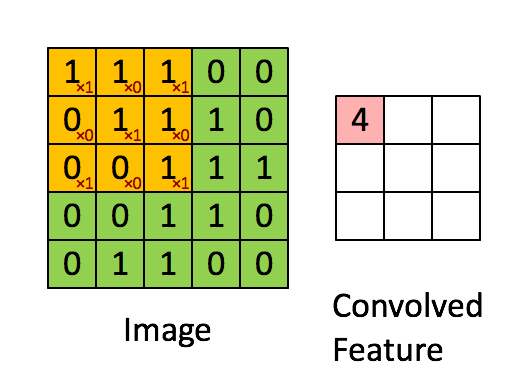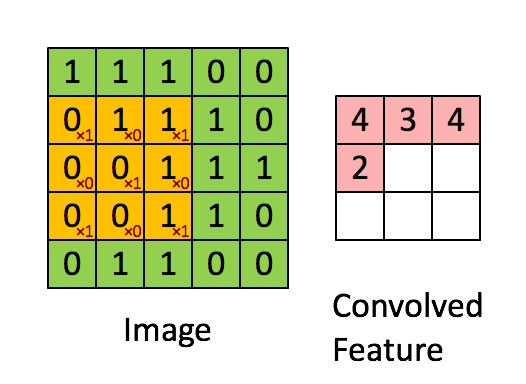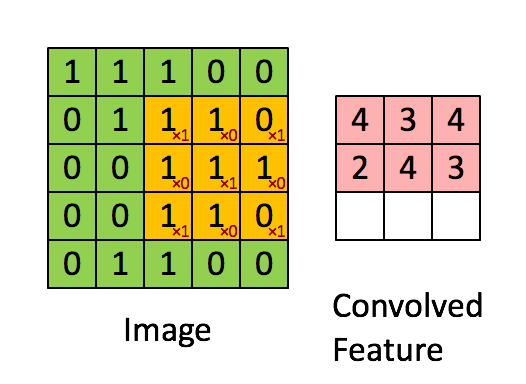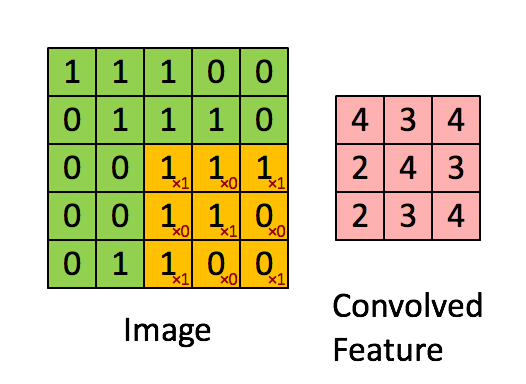
上边动图$i =5, k =3, p = 0$则卷积结果的列数$o = i - k + 1 = 5 - 3 + 1 = 3$。
- k旋转$180^{\circ}$后的$k'$和$k$不同的问题。看下面的程序,请计算卷积结果的第一个点数值是?
import numpy as np
from scipy import signal
i = np.array([[1,1,1,0,0],
[0,1,1,1,0],
[0,0,1,1,1],
[0,0,1,1,0],
[0,1,1,0,0]])
k = np.array([[1,0,1],
[1,0,0],
[1,0,1]])
o = signal.convolve(i, k, mode = "valid")
print o
执行结果:
[[4 3 3]
[3 4 3]
[3 3 3]]
程序结果第一个点的值是4。怎么来的?先将k旋转$180^{\circ}$。
1,0,1
0,0,1
1,0,1
然后和i的前3行前3列对应乘积并求和
1,1,1
0,1,1
0,0,1
计算如下:
1x1 + 0x1 + 1x1 +
0x0 + 0x1 + 1x1 +
1x0 + 0x0 + 1x1
= 4
如果程序里k没有旋转$180^{\circ}$(就按图的卷积方式直接计算或认为是某核旋转了$180^{\circ}$),那么参与计算的k为
1,0,1
1,0,0
1,0,1
然后和i的前3行前3列对应乘积并求和
1,1,1
0,1,1
0,0,1
计算如下:
1x1 + 0x0 + 1x1 +
0x1 + 1x0 + 1x0 +
0x1 + 0x0 + 1x1
= 3
换句话说如果将k变为:
1,0,1
0,0,1
1,0,1
那么卷积结果的第一个元素值为3。
import numpy as np
from scipy import signal
i = np.array([[1,1,1,0,0],
[0,1,1,1,0],
[0,0,1,1,1],
[0,0,1,1,0],
[0,1,1,0,0]])
k = np.array([[1,0,1],
[0,0,1],
[1,0,1]])
o = signal.convolve(i, k, mode = "valid")
print o
执行结果为:
[[3 3 4]
[2 3 3]
[2 2 4]]
总结:程序里的k应该是图里的k的旋转$180^{\circ}$值。
请分析一下:下图的核在程序里应该设计成什么样子?

图上所示卷积核似乎是
[[0,1,2],
[2,2,0],
[0,1,2]]
设计程序如下:
#coding:utf-8
import numpy as np
from scipy import signal
i = np.array([[3,3,2,1,0],
[0,0,1,3,1],
[3,1,2,2,3],
[2,0,0,2,2],
[2,0,0,0,1]])
k = np.array([[0,1,2],
[2,2,0],
[0,1,2]])
o = signal.convolve(i, k, mode = "valid")
print o
结果却是
[[18 20 19]
[10 9 17]
[11 8 14]]
18是咋算出来的?如果想程序和图一致,这里需要把图里的k旋转$180^{\circ}$,程序该为如下的样子:
#coding:utf-8
import numpy as np
from scipy import signal
i = np.array([[3,3,2,1,0],
[0,0,1,3,1],
[3,1,2,2,3],
[2,0,0,2,2],
[2,0,0,0,1]])
k = np.array([[0,1,2],
[2,2,0],
[0,1,2]])
o = signal.convolve(i, k, mode = "valid")
print o
print "*" * 20
k = np.array([[2,1,0],
[0,2,2],
[2,1,0]])
o = signal.convolve(i, k, mode = "valid")
print o
程序执行结果:
[[18 20 19]
[10 9 17]
[11 8 14]]
********************
[[12 12 17]
[10 17 19]
[ 9 6 14]]
星号下的输出结果和图片上的卷积结果一致!所以从图片上我们看到的卷积核和程序里的k是旋转了$180^{\circ}$的关系。
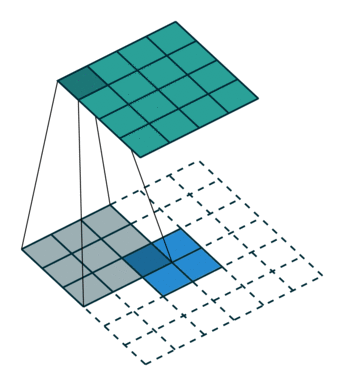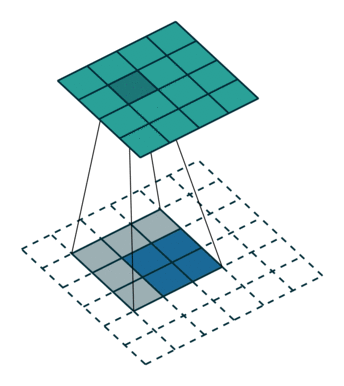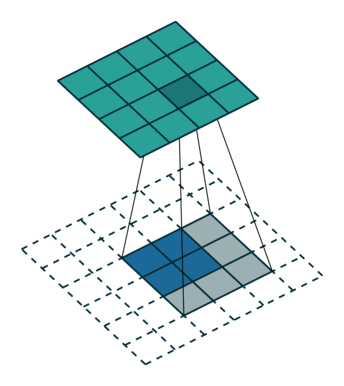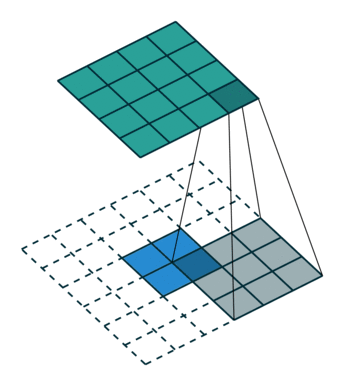
20.3 Half padding模式
same模式的卷积。same模式又称Half padding,意思是有$\lfloor \frac{k}{2} \rfloor$核在数据外部开始移动卷积,通常要求核的列数为奇数odd。卷积结果$o$和卷积的数据$i$形状一致,尺寸不发生变化。 $$ o = i + \lfloor 2\frac{k}{2}\rfloor - (k - 1) $$ 如果$k = 2m + 1$则: $$ o = i + 2 \lfloor \frac{k}{2}\rfloor - (k - 1) = i + 2m - (2m + 1 - 1) = i $$
same模式的卷积操作,滑动步长为1,输入数据图片大小为$i\times i$,卷积核大小为$k\times k$,卷积后图像大小:$i\times i$ 那么每边填充0的的列数$p = \lfloor \frac{k}{2} \rfloor$。 same模式卷积的特点是k核的中心与输入数据的每个数据对齐,对应求积之和作为该数据点的卷积数据。如果需要填0,尽量做到各边的填0的列数一样,但有的时候左右、上下边缘填0的行数或列数不一致,例如当k的列数是偶数的时候,这个和模块里的卷积函数的设计直接相关,考虑一般性,这里就不展开了,建议k的列数选奇数,因为深度学习的很多框架的卷积核都是奇数列。
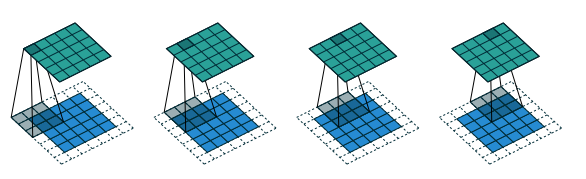
上图输入数据i为$5\times5$、核k为$3\times3$,则$p = \lfloor \frac{3}{2} = 1$填0列数,$o = 5 +2 \lfloor \frac{3}{2}\rfloor - (3 - 1) = 5 + 2 - 2 = 5$。
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
i = np.array([[1,1,1,0,0],
[0,1,1,1,0],
[0,0,1,1,1],
[0,0,1,1,0],
[0,1,1,0,0]])
k = np.array([[1,0,1],
[0,1,0],
[1,0,1]])
o = signal.convolve(i, k, mode = "same")
print o
执行结果:
[[2 2 3 1 1]
[1 4 3 4 1]
[1 2 4 3 3]
[1 2 3 4 1]
[0 2 2 1 1]]