18. Scipy Tutorial- 方波傅里叶分解与合成

周期性矩形波(方波)信号：在scipy中用signal包里的square函数来表示。signal里支持的内置其他波形函数可以到其官网查找。当然构造一个方波也可用numpy的zeros和ones来构建。

#coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
x = np.zeros(500)
x[100:150] = 1
plt.plot(x)
plt.ylim(-0.3, 1.3)
plt.show()

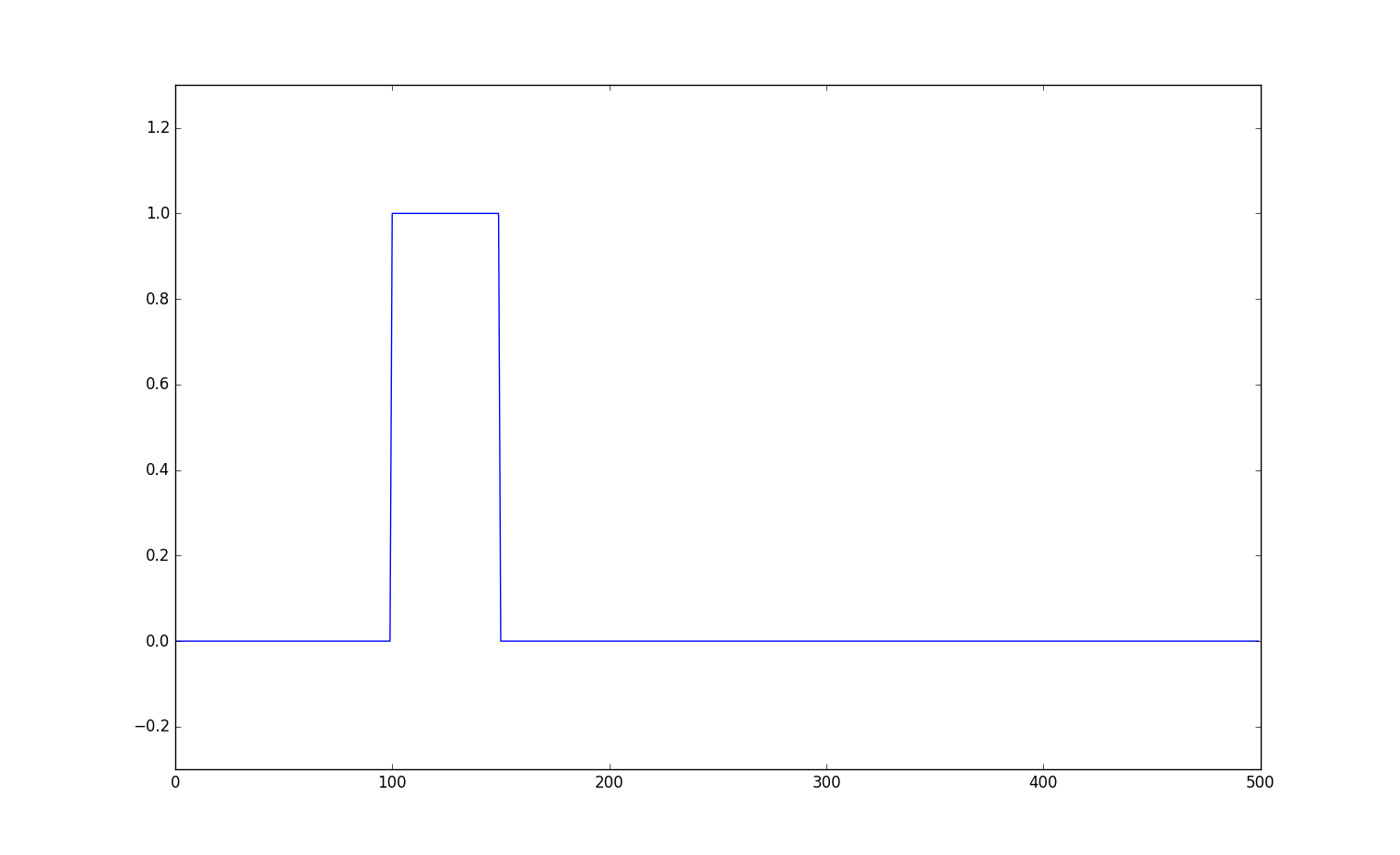根据傅立叶分析，任何信号都可以分解成一系列不同频率的正弦信号，方波中包含了非常丰富的频谱成分。下面可以用实验来直观的分析方波中的频率成分即fft，看看不同频率的正弦信号是如何叠加成为方波的即ifft。

#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
b = 30
f_s = 80
N = 8000
t = np.linspace(0, 10, N, endpoint=False)
sq = signal.square(2 * np.pi * 5 * t)

F = fftpack.fft(sq)
f = fftpack.fftfreq(N, 1.0/f_s)

F_filtered = F * (abs(f) < 5)
print "F_filtered", F_filtered
ift = fftpack.ifft(F_filtered)
mask = np.where(f >= 0)

fig, axes = plt.subplots(4,1)
axes[0].plot(t, sq)
axes[0].set_ylim(-2, 2)
axes[1].plot(f[mask], abs(F[mask])/N, label="freq")
axes[2].plot(t,ift.real, label="all")
axes[3].plot(t,ift.real, label="zoom")
axes[3].set_xlim(1, 2)
plt.show()

整个程序有三部分：

(1).利用scipy.signal包里的square函数生成方波。

sq = signal.square(2 * np.pi * 5 * t)

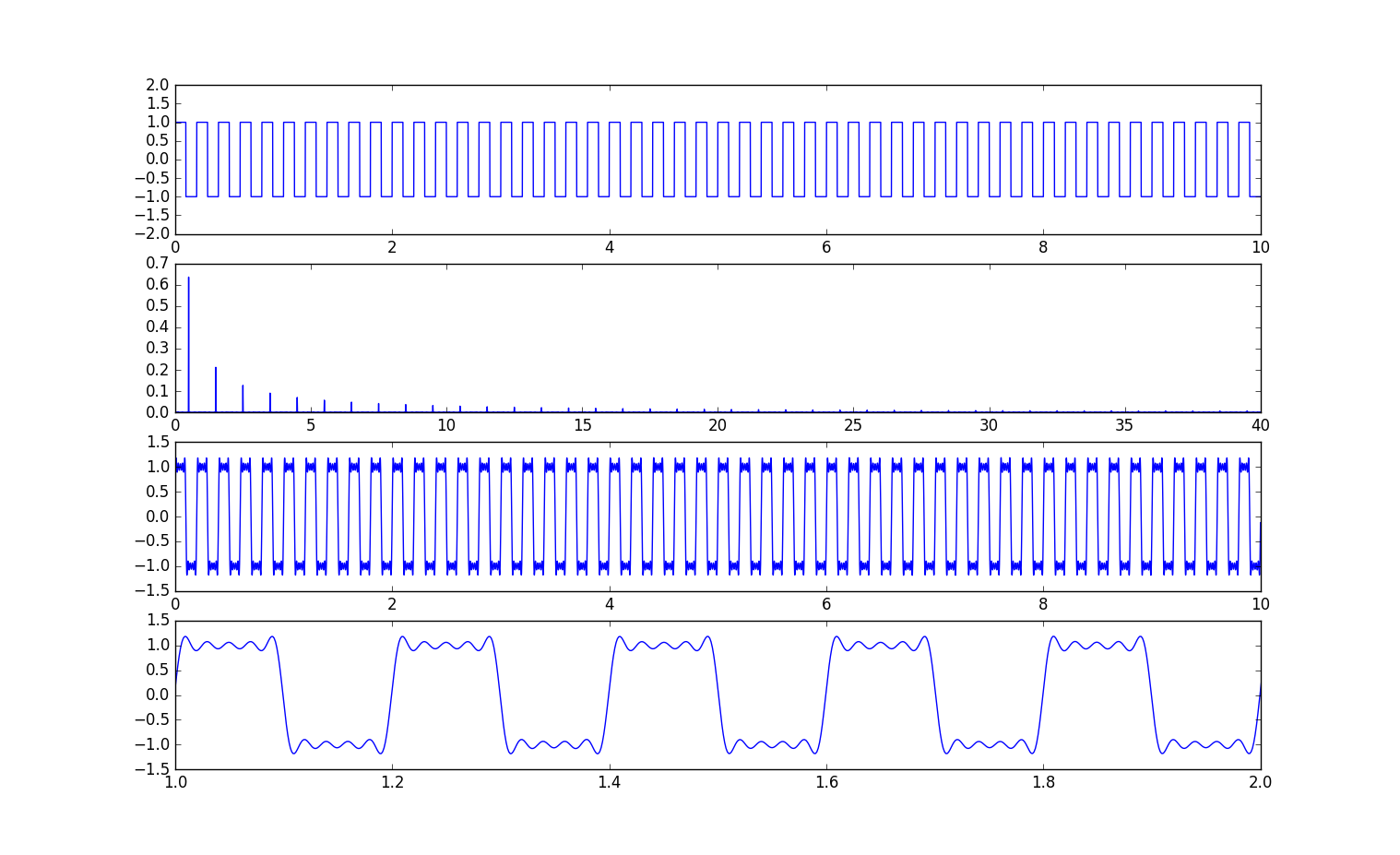
结果如下图子图1,最顶上的图。

(2).利用scipy.fftpack包里的fft对方波进行频谱分析，即分解得到若干个频率。

F = fftpack.fft(sq)
f = fftpack.fftfreq(N, 1.0/f_s)

可视化图为下图子图2,即第二个图。

(3). 利用scipy.fftpack包里的ifft快速傅里叶逆变化得到若干频率正弦波组成的时域信号。结果如下图子图3和4,子图4是对子图3的局部放大。